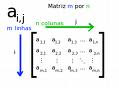
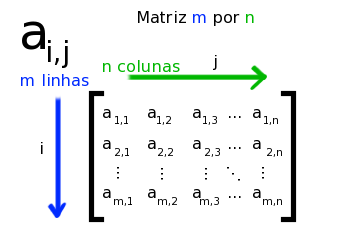
Definição: é uma tabela de elementos dispostos segundo linhas e colunas. Uma matriz A do tipo m x n, onde m é o número de linhas e n o número de colunas,
M x N ( lê-se m por n).
Obs.:
1- se em uma matriz o número de linhas é diferente do número de colunas então a matriz será dita como retangular (m ¹n).
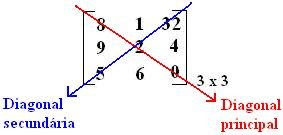
2- se em uma matriz o número de linhas é igual ao de colunas então a matriz será dita quadrangular (m = n) onde formam a diagonal principal da matriz.
3 – Uma matriz apenas é igual a outra se todos os seus elementos forem iguais e ocuparem as mesmas posições dos elementos da segunda.
Matrizes Importantes:
1-) Matriz transposta: é aquela onde as linhas se transformam em colunas e as colunas em linhas.
2-) Matriz oposta é aquela onde todos os elementos possuem sinais trocados.
3-) Matriz nula: é aqueles onde todos os elementos são iguais a 0 (zero).
4-) Matriz identidade ou unidade: é uma matriz quadrada onde os elementos da diagonal principal são todos iguais a 1 e os demais 0 (zero).
5-) Matriz diagonal: é uma matriz quadrada onde os elementos fora da diagonal principal são todos iguais a 0 (zero).
OBS: Matriz singular: é uma matriz diagonal onde os elementos da diagonal principal são todos iguais.
6-) Matriz triangular: é matriz quadrada onde todos os elementos acima ou a baixo da diagonal principal ou secundária são todos iguais a 0 (zero).
7-) Matriz linha: é aquela que possui apenas uma linha.
8-) Matriz coluna: é aquela que possui apenas uma coluna.
9-) Matriz simétrica: uma matriz quadrada é dita simétrica se ela é igual a sua transposta.
10-) Matriz anti-simétrica: uma matriz quadrada é dita anti-simétrica se sua oposta é igual a sua transposta
A Matriz é usada para da um resolução melhor,quanto mais m x n melhor a resoluçaõ da imagem, quanto menos m x n pior a resolução da imagem.
 Toda imagem é formada por matrizes, toda matriz é no minimo de ordem 1x1 ou seja 1 linha e uma coluna, em imagens o tamanho da matriz esta relacionado a sua resolução,quanto mais linhas e culunas mais nitida sera a imagem .
Toda imagem é formada por matrizes, toda matriz é no minimo de ordem 1x1 ou seja 1 linha e uma coluna, em imagens o tamanho da matriz esta relacionado a sua resolução,quanto mais linhas e culunas mais nitida sera a imagem .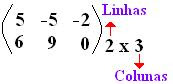.jpg)