Vida de Eluer .

Eluer nasceu em 15 de abril de 1.701 , na Suíça . Foi um grande matemático , que tambem amava a física , engenharia e astronomia , mais quem realmente fez com que ele tomase gosto pela matemática foi seu pai , que o encinou e dedicou muito tempo ao filho .
Assim Eluer recebeu seu primeiro mestrado aos seus 17 anos , mais tarde ele ganhou seu primeiro premio em uma competição numa academia de Paris , que assim ele conseguil ganhar por mais 12 vezes .
Mais em 1.735 ele perdeu a visão de um de seus olhos , assim ele teve qe se abituar e aprender a resolver as formulas mesmo ja a cada dia perdendo mais e mais de sua visão , terminando compretamente cego pelos seus 17 anos restante de sua vida , durante esse tempo sua produtividade somente almentou .
Eluer acabou morrendo vitima de um ''derrame'' aos seus 76 anos de idade , deixando assim a lembrança de um grande genio da Matamática :) .

Camila 2 ''B

Probabilidade no dia a dia

Probabilidade A probabilidade é a probabilidade que algo acontecerá. Por exemplo, quando você ouve o relatório do tempo na manhã, e o weatherperson diz-lhe que há uma possibilidade de 20% da chuva que estão dizendo que a probabilidade da chuva é 20%.
Alguns conceitos importantes a compreender aqui são que se houver uma probabilidade de 20% que chova, há uma probabilidade de 80% que não chova. As probabilidades não podem adicionar até mais de 100%, e a soma de todas as várias possibilidades deve adicionar até 100%.
Em casos simples como uma aleta da moeda, ou na possibilidade da chuva, onde há somente 2 possibilidades, as 2 probabilidades adicionarão a 100%. Em algumas situações entretanto haverá mais de 2 possibilidades. Se nós calcularmos somente algumas das probabilidades, não adicionarão até 100%, porque nós não consideramos todas as possibilidades, mas aquelas possibilidades existem ainda, e devem adicionar até 100% no total.
Uma outra maneira escrever a mesma informação deve dizer que há uma probabilidade do 2 da chuva, e que há conseqüentemente uma probabilidade do 8 que não chova. A probabilidade total não pode ser mais de 1, e uma vez outra vez todas as possibilidades devem adicionar até 1.
Esses são alguns exemplos de onde usamos probabilidade em nosso dia a dia.

Neste Bimestre aprendemos diversas coisas, como: probabilidade, análise combinatória, equações lineares, números binominais entre outros.
O que eu achei mais interessante foi Probabilidade, de acordo com minhas leituras, a probabilidade teve ínicio com os jogos de cartas, dados e de roleta. Esse é o motivo da grande axistência de exemplos de jogos de azar no estudo da probabilidade. A teoria da probabilidade permite que se calcule a chance de ocorrência de uma número em um experimento aleatório.

Amanda B.Sales Nogueira 2ºB

Permutação, Arranjo e Combinação

Combinação você usa quando quer agrupar coisas em que a ordem não importa, ou seja, só importa a variação. Por exemplo, você tem 5 Filmes e quer saber quantos grupos de 2 podem ser formados com eles, você faz combinação de 5 dois a dois; a ordem dos elementos não importa.Permutação é quando só importa a ordem, porque a Ordem não muda. Para saber quantas palavras podem ser formadas com as letras A, B, C e D, por exemplo. Deve-se fazer então permutação de 4 (4x3x2x1). A natureza não varia, são sempre os mesmos elementos em todas as opções.Por último, arranjo é quando tanto natureza quanto ordem influenciam.

Probabilidade: Definição

A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade.
Com a Probabilidade, é possível calcular a chance de determinado evento ocorrer.

Para resolvermos um problema de Probabilidade, podemos usar a fórmula:



Onde:
n(U) é o número de elementos do espaço amostral.
n(A) é o número de eventos.

Sendo assim, é só dividirmos o número de eventos pelo número de elementos do espaço amostral.
Abaixo, um exemplo:

Qual a probabilidade de:

Obtermos um número menor que 3 no lançamento de um dado?

Resolução:
n(U): 1,2 (os dois números menores que 3 que temos em um dado)
n(A): 6 (número de elmentos de um dado, seis números).



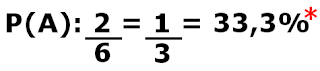
* Após fazer a divisão, multiplicamos o resultado por 100, para obtermos o por cento.

Resposta: A probabilidade de obtermos um número menor que 3 no lançamento de um dado é de 33,3%.

A ANÁLISE COMBINATÓRIA – Um resumo do 3º. Bimestre

Um pouco de História

Foi a necessidade de calcular o número de possibilidades existentes nos chamados jogos de azar que levou ao desenvolvimento da Análise Combinatória, parte da Matemática que estuda os métodos de contagem. Esses estudos foram iniciados já no século XVI, pelo matemático italiano Niccollo Fontana (1500-1557), conhecido como Tartaglia. Depois vieram os franceses Pierre de Fermat (1601-1665) e Blaise Pascal (1623-1662).

A ANÁLISE COMBINATÓRIA é um dos tópicos que a Matemática é dividida, responsável pelo estudo de critérios para a representação de quantidade de possibilidades de acontecer um agrupamento sem que seja preciso desenvolvê-los.
Na análise combinatória estudamos dentro do princípio fundamental da contagem:- Fatorial - Arranjos simples - Permutação simples - Combinação - Permutação com elementos repetidos


Um rapaz possui 4 bermudas e 4 camisetas. De quantos modos diferentes ele pode se vestir, com essas roupas?

“b” - bermuda

“c” - camiseta

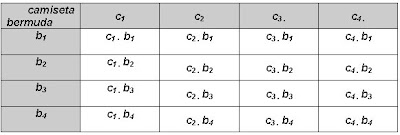O quadro mostra que existem 4 . 4 = 16 modos diferentes para o rapaz vestir suas roupas.



Fatorial (!)

Sendo n um número natural maior que 1, definimos como fatorial de n (n!) o número:
n! = n .(n-1) . (n-2) . ... .4.3.2.1
Lê-se n! como n fatorial. Observe os exemplos a seguir: 7! = 7 . 6 . 5 . 4 . 3 . 2 . 1 = 5040 3! = 3 . 2 . 1 = 6 Por definição, para n = 0, temos 0! E, para n = 1, 1! = 1

Permutação simples (Mudança de elementos)

Permutações simples Os arranjos simples, de classe n, de n elementos distintos são denominados permutações simples desses n elementos. Por exemplo, se A = {1, 2, 3}, as permutações simples de seus elementos são: 123, 132, 213, 231, 312 e 321.

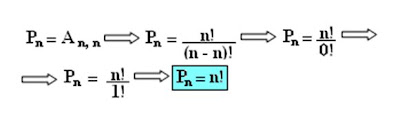
Permutações com elementos repetidos

Vamos considerar o número de anagramas da palavra Banana. Cada anagrama solicitado é uma permutação das letras B, A, N, A, N, A. Temos 6 letras; se todas fossem diferentes, teríamos P6= 6! = 720 anagramas.

Fixando a letra A em 3 dessas posições, assim teremos um único anagrama, pois há permutação de 3 letras. A entre se não cria novos anagramas.

Portanto o número de anagramas da palavra BANANA é:

Consideremos n elementos:
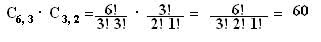
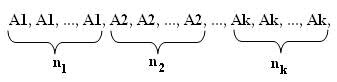O número Pn (n1: n2: ...: nk) de permutações desse elementos será calculado por: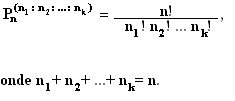

Arranjos Simples

Sendo A um conjunto com n elementos distintos e p um número natural, de modo que p ≤ n, denominamos de arranjos simples dos n elementos de A, tomados p a p, os agrupamentos ordenados de p elementos diferentes que é possível formar com os elementos de A. O número p é denominado de ordem ou classe do arranjo. Indicamos o número de arranjos de n elementos, p a p, por An,p ou Apn. A fórmula de arranjos simples é:

Combinações Simples

Sendo A um conjunto com n elementos distintos e p um número natural e modo que p ≤ n, denominamos de combinações simples dos n elementos, tomados p a p, os agrupamentos de p elementos distintos e que diferem entre si somente pela natureza de seus elementos. O número p é denominado classe ou ordem da combinação. O número de combinações simples, de classe p, de n elementos é denotado por Cn, p ou Cnp. A formula geral é:

Arranjo ou Combinação ?

Ao resolvermos uma situação problema de análise combinatória encontraremos um agrupamento, é nesse momento que aparece a seguinte dúvida: “esse agrupamento é uma combinação ou um arranjo?”.

É preciso identificar corretamente que tipo de agrupamento o exercício está trabalhando, para isso é possível utilizar o seguinte critério: Escrevemos um dos agrupamentos que o exercício sugere, mudamos a ordem dos seus elementos. A partir dessa mudança iremos concluir que:

• Será um arranjo se essa mudança alterar o agrupamento original, pois sabemos que um arranjo pode ser diferenciado tanto pela natureza de seus elementos como pela ordem desses elementos.

• Será uma combinação se essa mudança não alterar o agrupamento original, pois sabemos que uma combinação é um arranjo que se difere apenas pela alteração na natureza de seus elementos.

Veja o exemplo de como fazer essa verificação.

Exemplo: Um pintor, dispondo de cinco cores diferentes de tinta pretende misturar três delas, em quantidades iguais, para obter uma nova cor. Quantas novas cores ele poderá obter?

Verificando se os agrupamentos sugeridos são arranjos ou combinações: Vamos supor que as cinco cores que o pedreiro possui são: amarelo, branco, verde, vermelho, azul.

Escolhendo um dos agrupamentos formados pela combinação de 3 tintas teremos: {azul, amarelo, branco}, se mudarmos a ordem desses elementos {amarelo, branco, azul} não irá alterar o agrupamento, portanto os agrupamentos montados serão combinações simples. Pra encontrar a quantidade de combinações possíveis basta aplicar a fórmula:

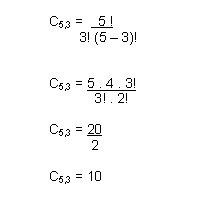
Portanto, é possível montar 10 combinações de 3 tintas com o grupo de 5 tintas

Probabilidades

Probabilidades

As probabilidades são uma maneira diferente de expressar a mesma informação, mas em uma maneira que seja frequentemente mais aplicável ao poker e a outros jogos gambling.

Quando a probabilidade for expressada como um número decimal, ou uma porcentagem, as probabilidades estão expressadas como 2 números separados por uns dois pontos tais como 5:1. Pela convenção esta notação indica que as probabilidades são 5 a 1 de encontro a ocorrer do evento.

Há umas maneiras diferentes de dizer a mesma coisa, e de explicar o que os números significam. No exemplo, deixe-nos supõem que o evento que nós estamos interessados dentro está começando 1 cartão particular que nós necessitamos a fim fazer nossa mão. A notação diz-nos que 5 vezes nós não começaremos o cartão que nós necessitamos, e 1 vez, nós começaremos o cartão nós necessitamos. Usar-se que o mesmo exemplo, nós começará o cartão que nós necessitamos 1 vez em 6 tentativas, ou 1/6.

Probabilidade e cotidiano

O estudo da teoria das probabilidades é um instrumento que nos ajuda a estimar com o máximo de precisão possível o resultado de eventos, os quais, antecipadamente, não poderíamos saber o resultado. Ela aplica-se a quase todos os campos da área do conhecimento humano.
O cálculo das probabilidades é utilizado em muitos ramos do conhecimento, mas principalmente na estatística, quando deseja se fazer interferências a respeito de uma população a partir de dados coletados numa amostra. Na Biologia, por exemplo, quando queremos saber previsões de caráter genético, na política ( previsões eleitorais) a probabilidade desempenha un papel importante.

Ex: Probabilidade Condicional ( Biologia )

Em alguns problemas de genética é preciso calcular a probabilidade de ocorrência de um evento sobre o qual já temos alguma informação.
Como nesse exemplo: Pais normais e heterozigotos , para o albinismo, tem uma criança normal. Qual a probabilidade de que essa criança seja heterozigota?

A criança em questão já nasceu e não é albina , certo? Então não podemos contar a probabilidade de ser aa , pois não tem essa possibilidade. Logo dos 3 encontros gaméticos possíveis temos 2/3 de ser heterozigota e 1/3 de ser AA.

DIFÍCIL.....

Oi amigos

Tenho certeza que vocês podem se esforçar mais um pouco.

Esse assunto está muito difícil de ser entendido por leitores do blog. Que tal usar exemplos da vida diária? Alguns fizeram isso, parabéns!!!

Tentem pesquisar sobre o assunto e não coloquem fórmulas, pois sabem bem como elas são " chatas" quando não são muito bem entendidas.

Tem a pesquisa sobre os geômetras. MÃOS A OBRA.

Um abração a todos...
Sara

Neste terceiro bimestre aprendemos muitas coisas , diversas , vou citar uma como por exemplo estudamos neste finalzinho de bimestre os ’ Números binominais ‘ juntamente com todo o restante que foram as Equações lineares , probabilidades e tantas outras .
Vou fazer um breve comentário aqui sobre o que eu realmente entendi ,sobre os números binominais .
Sabemos que os números de combinações simples, de classe p, com N(numero) elementos é constituído , esse número também é chamado número binominal ou número combinatório.

um ex; as letras P/n são as chamadas de
binominal de N sobre P. (n)=n!
(p) p!(n-8)!
N é o numerador e P é o denominador.

Ou seja resumindo tudoo os dois números naturais que são N e P são os chamados de binominais que sempre indicamos por (P/N)

Já os complementares são distinguidos da seguinte forma , Ex: p+q=N
Ou seja eles são complimentares quando por ex ocorre 5/3 e 5/2
3+2=5 .
Ou seja resumindo tudo os dois números naturais são N e P , qe são chamados de binominais .

Bem assim termino meu assunto .
Postei aqui da maneira que eu entendi e espero qe vocês tmbem tenham se interesado e tenham intendido tambem .

Probabilidade

O assunto que eu achei mais interessante foi Probabilidade.Um caso de probabilidade é o do dado,onde vc pode calcular o quanto de chances de cair os números que somados dão 11, por exemplo,a parte de espaço amostral também onde vc mostra o total de possibilidades,e o evento,que mostra,por exemplo a quantidade de números que dão a soma 8!!!!

PERMUTAÇÃO SIMPLES e ARRANJO SIMPLES.

Ola eu vo falar o que eu entendi de PERMUTAÇÃO SIMPLES e ARRANJO SIMPLES:
Permutação é um tipo de arranjo simples. Assim, relembrando que arranjo simples é um subconjunto de um conjunto A de n elementos. Os elementos que formam os arranjos podem se diferenciar pela natureza ou pela ordem de seus elementos.
fui isso que eu entendi de permutação simples e arranjo simples..

xauuu.....bjsssssss

Oi,bom o assunto que escolhi para falar é PERMUTAÇAO SIMPLES!!!
permutaçao simples,e uma ato de permutar coisas ou seja mudar algo de ordem atraves
de contas!!!! que tambem e chamado de arranjo simples
No começo esse assunto foi um pouco dificil para mim ,mas aos poucos
consegui entender!!!
A permutaçao simples e tambem realizada por meio de sempre diminuir uma casa de um numero relacionado uma palavra por exemplo a palavra amor!!Quantos anagramas podemos formar com essa palavra??/ um todos podem pensar que e dificil mas nao e!!!veja como e feito!!!
bom primeiro fazemos tambem seu arranjo e nada mais nada menos que o ato de multiplicar seu numero de letras!!
AMOR=SAO 4 letras 4.3.2.1.=24,, este e seu arranjo!!!!!!!!!
E sua permutaçao seria
p={amor,amro,arom,armo,aorm.aomr,maro,maor,mroa,mrao,mora,moar,oamr,oarm,orma,oram,omar,omra,ramo
raom,rmoa,raom,roma,rmao,}e ha tambem sua formulade arranjo simples (An,p=n!
(n-p)!

Bom todos essas palavras sao suas permutaçoes!!!!foi isso que todos aluno do 2colegial aprenderam com a professora CAROLINA!!!!!

Probabilidade: Espaço amostral

Espaço Amostral ou conjunto universal é o conjunto U de todos os resultados possíveis de um experimento aleatório. O número de elementos desse conjunto é indicado por n(U).




Dados dois eventos A e B de um Espaço Amostral S a probabilidade de ocorrer A ou B é dada por: P(A U B) = P(A) + P(B) – P(A ∩ B) Verificação: O Número de elementos de A U B é igual à soma do número de elementos de A com o número de elementos de B, menos uma vez o número de elementos de A ∩ B que foi contado duas vezes (uma em A e outra em B).

∩ significa intersecção
U significa união

Análise Combinatória

Permutação : Permutação trata de analisar de quantas maneiras podemos organizar um grupo de n elementos, usando os n elementos. Por exemplo, imaginemos um ônibus com 3 lugares vazios para 3 amigas se sentarem. De quantas maneiras distintas eles podem se sentar? No primeiro assento, podem se sentar 3 pessoas diferentes. Já no segundo, apenas 2 pessoas diferentes poderão se sentar, pois já existe uma pessoa no primeiro assento. No último assento, somente um poderá sentar, pois os outros dois assentos já estarão ocupados. Podemos acompanhar este raciocínio, dando nomes para as pessoas: Cláudia, Ana e Jéssica. Primeiro assento ocupado por Cláudia: C-?-?. Restam 2 lugares. Cláudia está fora. O segundo assento poderá ser ocupado por 2 pessoas. Segundo assento ocupado por Ana: C-A-?. Restou uma pessoa e um assento. Obviamente, C-A-J.

Segundo assento ocupado por Ana: C-A-?. Restou uma pessoa e um banco. Obviamente, C-A-J. Primeira poltrona ocupada por Ana: A-?-?. Mesmo raciocínio de Cláudia. Primeiro assento ocupado por Jéssica: J-?-?. Mesmo raciocínio de Cláudia. Como o raciocínio do primeiro assento se repete, assim sabe-se que o calculo é 3 x 2. consequentemente sabemos que para o segundo assento, o cálculo é 2 x 1. O cálculo da permutação é então 3 x 2 x 1 o que é igual a : 6 maneiras distintas das três se sentarem.

A fórmula é: Permutação(n) = n*(n-1)*(n-2)*....

Este tipo de multiplicação é chamado de fatoração e é representado pelo ponto de exclamação(!).

Então, temos:

Permutação(n) = n!

e

n! = n*(n-1)*(n-2)*...

Esse bimestre eu aprendi Sobre Análise combinatória....


O estudo da análise combinatória nos permite descobrir quais são as diferentes possibilidades de uma combinação de variáveis. Por exemplo, quantas placas de carro são possíveis de existir no sistema atual de placas brasileiro. É uma matéria bastante cobrada em vestibulares e concursos públicos, pois envolve um pensamento mais abstrato, pois na maioria das vezes, não enxergamos todas as possibilidades. A explicação dessa matéria é muito mais fácil quando utilizamos exemplos.
Então, supondo que um restaurante tenha disponível 2 tipos de bifes, 2 tipos de arroz, 2 tipos de feijão e 3 tipos de bebidas.
O dono do restaurante queira servir pratos contendo 1 elemento de cada tipo de comida. Nomeando os tipos de comida da forma "bife 1, arroz 1, arroz 2 ... bebida 1, bebida 2, etc",





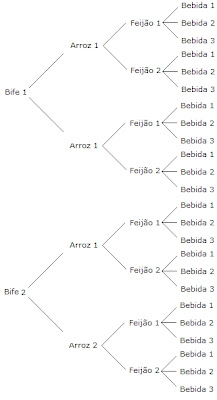
Mas podemos calcular de forma diferente. Basta multiplicar todas as opções de comida disponiveis: 2 . 2 . 2 . 3 = 24.

Análise Combinatória

Problemas que envolvam o cálculo do número de agrupamentos que podem ser feitos com os elementos de um ou mais conjuntos, submetidos a certas condições, são resolvidos por meio de assuntos que constituem a análise combinatória.


Permutações

Permutações simples



Os arranjos simples, de classe n, de n elementos distintos são denominados permutações simples desses n elementos.


Indicamos por Pn o número de permutações simples de n elementos:


Pn= n(n-1) . (n-2) . ... .3.2.1

e

P=n!



Permutações com elementos repetidos


A permutação de n elementos dos quais a são um tipo s de outro e b de outro, com a= s + b, é dada por:


P a,s,b ___n!___

n a! s! b!

Ex: Quantos anagramas tem a palavra BATATA?

____P6!____

P3.P2

____60!____= 60

3!2!

Sendo assim, a palavra BATATA tem 60 anagramas.

Arranjo Simples

São os agrupamentos ordenados diferentes que se podem formar com p dos n elementos dados.

Indica-se por An,p e Ap

n

Calculamos o total desses agrupamentos assim:

An,p = n. (n-1). (n-2). ... .(n-p-1)

ou

An,p =___n!___

(n-p)!

Combinação Simples

Combinação simples de n elementos tomados p a p ( com p menor ou igual a n) são os subconjuntos com exatamente p elementos que se podem formar com os números dados.

Indica-se por Cn,p o número total de combinações de n elementos. Calcula-se por:

Cn,p = ___n!___

p!( n-p)!

Análise Combinatória

Permutação simples.

Neste 3º bimestre eu aprendi permutação simples, um assunto muito interessante e simples.



Permutações são os agrupamentos de um determinado número de elementos variando apenas a sua ordem. Ex.:
XYZ, XZY, YXZ, YZX,ZXY, ZYX.
O número de agrupamentos de uma permutação simples de n elementos é dado por n!.
P(m) = m(m-1)(m-2)...(m-p+1)...3.2.1
Ex.: De quantas formas podemos agrupar as sete cores do arco-íris? R: 7! = 5040
Como o uso de permutações é muito intenso em Matemática e nas ciências em geral, costuma-se simplificar a permutação de m elementos e escrever simplesmente:
P(m) = m!
Este símbolo de exclamação posto junto ao número m é lido como o fatorial de m, onde m é um número natural.
Embora zero não seja um número natural no sentido que tenha tido origem nas coisas da natureza, procura-se dar sentido para a definição de fatorial de m de uma forma mais ampla, incluindo m=0 e para isto podemos escrever:
0!=1

arranjos e combinaçoes

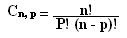
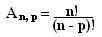
Hoje eu vou explica um pouco do que aprendi:
COMBINAÇÕES

Combinações:É sendo (A)um conjunto com(N)elementos distintos e (P)número natural e modo que (P)<(N),assim denominamos a combinação simples.
Exemplos:
1)Quantas equipes de 3 astronautas podem se formados com 20 astronautas?
resp: c,(n,p)= 6! = 6*5*4!=30 = 15
4!(6-4) 4!2! 2
è possivel formar 15 equipes de astronautas.

2) Numa prova de 10 questoes o aluno deve resolver apenas 6.De quantas maneiras diferentes ele poderá escolher essas 6 questões?
resp:C(n,p)= 30! = 30*29*28*27*26*25*24!= 142.506
6!(30-6)! 6! 24!

Os dois numeros 24 vc pode cortar eles,
nisso vc fatora o 6 e divide pela multiplicação de cima


essa sao as formulas a serem usadas
por combinação e arranjos simples









francini 2°B

PESQUISA

Procure saber as trajetórias de vida dos Geômetras: PITÁGORAS e TALES

Obs: Como já era de costume: não vale tirar cópias da Internet, nem postar atividades iguais às dos colegas.

POSTEM SUAS PESQUISAS LOGO, POIS TALVEZ DÊ TEMPO DE SEREM COMPUTADAS NO 3º BIMESTRE.

Um abração a todos.