O estudo da análise combinatória nos permite descobrir quais são as diferentes possibilidades de uma combinação de variáveis. Por exemplo, quantas placas de carro são possíveis de existir no sistema atual de placas brasileiro. É uma matéria bastante cobrada em vestibulares e concursos públicos, pois envolve um pensamento mais abstrato, pois na maioria das vezes, não enxergamos todas as possibilidades. A explicação dessa matéria é muito mais fácil quando utilizamos exemplos.
Então, supondo que um restaurante tenha disponível 2 tipos de bifes, 2 tipos de arroz, 2 tipos de feijão e 3 tipos de bebidas.
O dono do restaurante queira servir pratos contendo 1 elemento de cada tipo de comida. Nomeando os tipos de comida da forma "bife 1, arroz 1, arroz 2 ... bebida 1, bebida 2, etc",
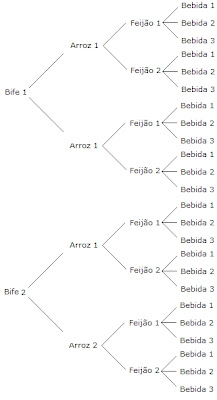
Mas podemos calcular de forma diferente. Basta multiplicar todas as opções de comida disponiveis: 2 . 2 . 2 . 3 = 24.
4 comentários:
Neste bimestre aprendemos:
'Permutações simples'
Ex;
PERMUTAÇÃO
Denominamos permutação de n elementos dados a toda sucessão de n termos formada com os n elementos dados.
Todo problema onde apenas a ordem em que os elementos aparecem distingue os agrupamentos é empregado o conceito de permutação.
Definimos por permutação a expressão abaixo :
Pn = n !
'COMBINAÇÃO'
Denominamos combinações de n elementos distintos tomados k a k aos conjuntos formados de k elementos distintos escolhidos entre os n elementos dados.
Todo problema onde a ordem dos elementos não importa é empregado o conceito de combinação.
Definimos por combinação a expressão abaixo :
Cn , k = n!
-----
k! (n-k)!
Neste bimestre aprendemos:
'Permutações simples'
Ex;
PERMUTAÇÃO
Denominamos permutação de n elementos dados a toda sucessão de n termos formada com os n elementos dados.
Todo problema onde apenas a ordem em que os elementos aparecem distingue os agrupamentos é empregado o conceito de permutação.
Definimos por permutação a expressão abaixo :
Pn = n !
'COMBINAÇÃO'
Denominamos combinações de n elementos distintos tomados k a k aos conjuntos formados de k elementos distintos escolhidos entre os n elementos dados.
Todo problema onde a ordem dos elementos não importa é empregado o conceito de combinação.
Definimos por combinação a expressão abaixo :
Cn , k = n!
-----
k! (n-k)!
Probalidade: Espaço Amostral
Esse bimestre um dos assustos que eu aprendi também foi Espaço Amostral; Espaço amostral é o conjutno universo denominado de (U) de todos os resultados possiveis de um experimento aleatório. O numero de elementos desse conjunto é indicado por n(U).
Por exemplo: nO lançamento de um dado U= {1,2,3,4,5,.} = esses são todos resultados possiveis
e n(U)= 6 = numero de elementos desse conjunto.
Para determinar o espaço amostral do experimento aleatório lançamento simultâneo de duas Moedas é simples;
Podemos indicar por exemplo
C pra cara e f para Coroa;
U= (C,C),(C,F),(F,C),(F,F)
n(U)= 4
Essas são todas as probalidades do espaço amostral acontecer no lançamento de uma moeda.
bom foi issO que eu pude entender com as aulas de probalidade.
Obs: postei aki por comentario pois não consegui postar normal, não sei o que aconteceu!.
Gabi, que tal mudar a cor dessa letra?
Ficou muito escura, lembra que sou meio ceguinha...
Abraço
Postar um comentário