sexta-feira, 16 de maio de 2008
SARA ESTE ANO ESTAMOS INOVANDO AS AULAS
DE MATEMATICA!!!!
AULAS MAIS PRODUTIVAS ESTAO SENDO DADAS P OS ALUNOS
estou começando a me entender com as aulas de matematica
esse blog so serviu para estimular o que ja havia sendo feito pela sara
esse ano acho que sera o melhor de todos!!!!!
e isso so ira me ajudar cada dia mais e mais!!!!!
estou ate gostando ate um pouco da materia
que antes para mim era muito
confusa e complicada!!!!!!
mas hoje sei que com sua ajuda
serei melhor em matematica.
obrigada!!!!!!
quinta-feira, 15 de maio de 2008
Planetário.
Vejam o que descobri:
Júpiter é o quinto planeta a partir do Sol e o maior de todos:
distância do Sol: 778.330.000 km (5,20 u.a)
diâmetro equatorial: 142.984 km; diâmetro polar: 133.708 km
massa: 1,900e27 kg
Júpiter tem duas vezes mais massa que todos os outros planetas juntos (318 vezes a massa da Terra). Júpiter é o quarto objeto mais brilhante no céu (depois do Sol, Lua e Vênus; em alguns períodos, Marte é também mais brilhante). É conhecido desde os tempos pré-históricos. A descoberta de Galileu, em 1610, das quatro luas de Júpiter, Io, Europa, Ganimédes e Calisto (hoje conhecidas como luas Galileanas), foi a primeira constatação de um centro de movimento que, claramente, não estava centrado na Terra. Esse foi um ponto significativo a favor da teoria heliocêntrica de Copérnico; Por defender abertamente a teoria de Copérnico, Galileu foi aprisionado a mando da Inquisição, forçado a abjurar suas crenças e condenado ao cárcere pelo resto de sua vida.
Júpiter foi visitado pela primeira vez pela sonda Pioneer 10 em 1973 e, mais tarde, pelas sondas Pioneer 11, Voyager 1, Voyager 2 e Ulysses. A sonda Galileu está atualmente viajando em direção à Júpiter. Os planetas gasosos não têm superfícies sólidas, seu material gasoso simplesmente tornar-se mais denso com a profundidade (os raios e diâmetros dos planetas são para níveis correspondentes a uma pressão de 1 atmosfera). O que vemos quando olhamos para esses planetas é o topo das nuvens em suas atmosferas (ligeiramente acima do nível de 1 atmosfera). Júpiter é cerca de 90% hidrogênio e 10% de hélio, com traços de metano, água, amônia e "rochas". Isso aproxima-se muito da composição da Nebulosa Solar primordial da qual todo o sistema solar se originou. Saturno tem uma composição similar, mas Urano e Netuno têm muito menos hidrogênio e hélio. Nosso conhecimento do interior de Júpiter (e de outros planetas gasosos) é essencialmente indireto, e é provável que permaneça assim por muito tempo. A sonda atmosférica Galileu penetrará apenas até próximo ao nível de 25 bar antes de perder contato com a Terra. Júpiter provavelmente tem um núcleo de material rochoso, algo em torno de 10 a 15 massas terrestres. Acima do núcleo fica o principal constituinte da composição do planeta - hidrogênio metálico em forma líquida. Essa forma exótica do mais comum dos elementos é possível somente a pressões superiores a 4 milhões de bars, como é o caso das camadas interiores de Júpiter (e Saturno). O hidrogênio metálico líquido constitui-se de elétrons e prótons ionizados (como o interior do Sol, mas a uma temperatura bem mais baixa). À temperatura e pressão do interior de Júpiter, o hidrogênio é um líquido, não um gás. É um condutor elétrico e a fonte do campo magnético de Júpiter. Essa camada provavelmente também contém alguma quantidade de hélio e traços de vários "gelos".
1º BIMESTRE .
E para melhor compreendermos, o livro nos propõe que façamos o estudo das razões trigonométricas através do círculo trigonométrico, o qual fizemos juntamente com a professora em sala de aula. E foi utilizando o círculo trigonométrico, que pudemos construir os gráficos do seno e cosseno.
Neste bimistre também aprendemos: Raio, Radiando, Comprimento da circunferência, Área da circunferência, e vários outros elementos da trigonometria. Quase toda a matéria do livro nos aprendemos, foram poucas coisas que não chegamos a ver.
Particularmente, gostei muito da maneira de ensinar da Profª Sara, conseguiu nos passar as informações mais importantes, de uma maneira resumida.
quarta-feira, 14 de maio de 2008
Pois a Professora Sara está tirando a rotina das aulas e sempre inovando, sempre mudando sua aula, e assim não ficando repetitiva as aulas o que anima muito os alunos, até alunos que não faziam nada estão fazendo, todos aprendem muito na aula da Sara, são poucos os professores hoje em dia que tem tanta qualidade pra fica inovando nas aulas, toda aula tem coisa nova, um dia é na informática, outro na sala de aula, mas com lições diferentes e assim por diante.
Em minha opinião na sala de informática é onde os alunos mais aprendem e participam das aulas, e assim a qualidade intelectual dos alunos só crescem, estou aproveitando muito nas aulas de Matemática
Aulas de matemática
tudo o que está no livro.
Exemplos:Graus,triangulos,lados,radianos,angulos e etc.
E com as explicações da professora e do circulo trigonométrico consequimos aprender,e a compriender tudo o que foi explicado.
Excelente trabalho!
A utilização desses novos meios é importantíssima dando uma aula mais dinâmica, interessante, deixando de lado aquele “bicho de sete cabeças” como é conhecida por alguns a matemática.
circulo trigonométrico
O circulo trigonométrico é passa por dois eichos chamados de eicho x e eicho y cos é o eicho x e sen é o eicho y para sabe a medida da circunferencia precisamosdos angulos que são 30,45,60,90 e vai até 360 paraq voce sabem as medidas dos anguloas voce precisa das formulas do sen e do cos.
Aulas de Matematica 1°Bimestre!!
No 1° Bimestre nós aprendemos muitas coisas interessantes e Revisamos outras..apesar da nossa classe não ser muito comportada, deu pra tirar duvidas sobre Trigonometria, sobre o PI radiano, Arcos trigonométricos pois eu tinha varias duvidas na 8° serie e no 1° colegial.. A professora tem muitos jeitos de dar aulas divertidas, eu aprendi me divertindo na sala, e isso foi muito bom, pois deu para tirar duvidas..Nós fomos para a Informática,eu gostei de Mexer no Programa Cabri Geometre,apesar de ainda não saber mexer direito. Mas eu gostei muito pois nós só ficávamos na sala, e isso muitas vezes era chato pois são 6 aulas por dia 6 aulas na classe ninguém merece, mas com a oportunidade de sairmos da sala e ir pra Informática era muito divertido. Eu gostei pois alem de tudo isso eu aprendi varias coisas que me ajudarão na hora de fazer um Vestibulinho, um ENEN.. E em nossas Vidas pois a matemática esta em tudo. .
Eu espero que no 2° Bimestre seja tão bom quanto o 1°..
Sobre as aulas de matemática...
Bom, esse bimestre trabalhamos várias coisas, primeiro começamos com o jornal, apesar de ser muito complicado, com as explicações em sala de aula sobre: Crescimento, decrescimento, proporcionalidade; Grandezas proporcionais e representações gráficas; Relacionando e analisando grandezas (tabelas); Análise e interpretação de gráficos; Função afim; Função quadrática; Simetria; Inequações; etc, consegui aprender e fazer uma boa prova. Assim que terminamos as atividades do jornal começamos as atividades do livro, em muito pouco tempo conseguimos trabalhar 55 páginas e aprendemos muito também, estudamos : ângulos, seno, cosseno, tangente, medida da circunferência, radiano, gráficos das funções seno e cosseno, além disso que aprendemos em sala de aula, fomos para sala de informática e lá reforçamos o conteúdo dado em sala de aula com os gráficos feitos no Cabri Geometre, isso fez com que as aulas não ficassem cansativas, chatas e nos trouxe muitos benefícios em relação ao aprendizado.
Comentário por: Felipe - 2º B
Função quadrátitca
que nós trabalhos muito também foi função quadrática.
Função quadrática é uma função dada por f(x) = ax2 + bx + c,
nas aulas de informatica fizemos bastante graficos relacionado
a isso, aprendi que grafico de uma função quadrática é chamado de "Parábola",
que é um desenho que forma com a concavidade virada para cima ou para baixo.
lembrando que se, * a>0, a parábola tem a concavidade voltada para cima; e se
*a<0 , a parábola tem a concavidade voltada para baixo
Para conseguimos fazer um grafico desse, temos que Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.
Bom, foi isso que eu entendi, sobre os graficos de funções quadráticas.
Conteudo de livro..
Para entendemos melhor o seno,cosseno,medir arcos,trigonométria.
Em sala de aula agente fez um arco onde envolvia tudo isso.
E foi muito mais facil de entender,cada execicio
E tambem, pude observar que eles estão presentes no nosso dia-á-dia em quase todo o lugar.
O livro deu uma grande ajuda pois com os desenhos e exercicios foi muito bom!!!!!!!!!!!
o Uso de seno e cosseno
esta falando de um assunto que foi bem trabalhado
nas aulas de matemática, seno e cosseno.
Desde então, pude observar que eles estão presentes
no nosso dia-á-dia em quase todo o lugar, por exemplo
nas janelas de sua casa , podemos reparar que ela faz
o desenho do triângulo que usamos para aplicar seno e cosseno,
e também posso da como exemplo uma escada, se voce quiser medir
a altura dela e lagura, também pode aplicar seno e cosseno, fomando um triâgulo
Enfim, são coisas simples que usamos no dia-á-dia mais que as vezes passam despercebidos pos nós, e que com as aulas de matemática sobre esse assunto eu pude perceber.
aulas de matemática
Radiano, Determinação de Quadrantes
A circunferencia unitaria pois tem raio 1 unidade de compromento o sentido positivo e o ant-horario.
Para saber isso é so saber em que quadrante esta sua 1ª determinação.
::Danilo Augusto 2°B
Arco Geometrico, Arco e Angulo Central, Comprimento e Medida de Arco
Em todos od Arcos de circunferencia tem um angulo central que fica no meio da circunferencia.
A medida do Arco é a mesma medida do angulo central. Para medir Arcos sempre usam unidades como: o grau e o radiano.
Aulas de Matemática
Círculo trigonométrico

Aulas de Matematicas..
Eu espero que no 2° Bimestre seja tão bom quanto o 1°..
aulas de trigonometria

A trigonometria é um dos modos de intender o que é a matematica eu me chamo Francini do 2°B, eu nao sabia nada de matematica morria de medo de repetir de ano mas chegou a professora Sara ensinando super bem agora eu sei a importancia da aula tanto de matematica como outras gostaria de imformar algo importante nao deixe as zueira te levar para o mau caminho estude porque sera a hora se voce aprender o que falta ESTUDE!!!!!
NESSE DESENHO QUE EU FIZ INDICA UMA CIRCUNFERENCIA E NELA MOSTRA QUE TEMOS QUE REPARTIR EM 4 PARTES E NELA TEMOS OS ANGULO DE 0° A 360°.
terça-feira, 13 de maio de 2008
Melhores Aulas.
O que mais me ajudou foi a utilização do Pi, entendi melhor ele e ainda conheci o Pi radiano, o que se usa muito na trigonometria para achar uma medida certa de uma circunferência e também sei diferenciar o Beta, com o Alfa e o Teta, o que me confundia bastante. Mexer com compasso e transferidor foi muito bom e ter contruido ângulos, foi ótimo ter lembrado disso e de ter descoberto coisas novas neles. A trigonometria é muito importante para que possamos calcular medidas de ângulos.
Tudo parece que foi resolvido, quando eu olhava os exercícios, eu pensava que era algo muito complicado
 e difícil, mais é uma das atividades mais simples da matemática.
e difícil, mais é uma das atividades mais simples da matemática.As aulas de Informática foram muito bem elaboradas. Gostei de aprender a mexer no Cabri Geometre, é um programa muito importante na construção de gráficos, montamos usando o seno e cosseno em nossas aulas e foi muito interessante ter mexido com esse programa, baixei ele em casa para poder fazer os meus trabalhos.
- Com certeza nesse bimestre, as aulas de matemática acrescentaram conteúdos que irão me ajudar muito em um Vestibulinho, no ENEM, no Vestibular e em qualquer outra prova. A trigonometria tem que ser entendida, pois ela sempre está presente em nosso dia-a-dia, é só percebermos que estamos praticando ela, assim como a sombra de um poste, ou a construção de uma casa, e estamos sempre vendo, e se entendermos tudo o que ela quer nos ensinar, com certeza será muito útil em nossas vidas.
aulas interesantes ...
E isto nos ajudou muito pois a única formula que
Precisamos decorar é a do Seno ,Cosseno e Tangente.
Na trigonometria usamos muito o PI rad, achar uma medida certa da circunferência ,para fazer todas estas atividades temos que saber que uma circunferência tem 360° exatos.
Também aprendemos que o rad é um arco cujo o comprimento é igual ao raio da circunferência transferido de lugar .
O que eu aprendi nas aulas de Matemática
Vou falar o que eu aprendi nas aulas de matemática, as aulas de matemática foram muito interessantes, achei importante os gráficos de seno e cosseno, exemplo de um gráfico de seno
,http://images.google.com.br/imgres?imgurl=http://modulos.math.ist.utl.pt/img/figuras/PictSin.jpg&imgrefurl=http://modulos.math.ist.utl.pt/html/SenoCoseno2.shtml&h=220&w=460&sz=38&hl=pt-BR&start=4&sig2=uO7Fgk54tkN6EJEt53KfLw&tbnid=ct111hY3f2ZvWM:&tbnh=61&tbnw=128&ei=9uwpSObiEYO0hAK4wYyaBw&prev=/images%3Fq%3Dgraficos%2Bde%2Bseno%26gbv%3D2%26hl%3Dpt-BR%26sa%3DG
O exemplo de outro gráfico de cosseno,
http://images.google.com.br/imgres?imgurl=http://www.cepa.if.usp.br/e-calculo/funcoes/trigonometricas/fcosseno/img_fcosseno/imagem1.gif&imgrefurl=http://www.cepa.if.usp.br/e-calculo/funcoes/trigonometricas/fcosseno/fcosseno.htm&h=352&w=397&sz=2&hl=pt-BR&start=17&sig2=3sWscHx0a9d8GE7hE2z6AA&tbnid=5BV70SENX2TgrM:&tbnh=110&tbnw=124&ei=me0pSPi1BZG-hALXqJSaBw&prev=/images%3Fq%3Dgraficos%2Bde%2Bcosseno%26gbv%3D2%26hl%3Dpt-BR%26sa%3DG
Esses são uns exemplos.Também achei enteressantes quando trabalhamos com Arco Côngruos, exemplo.
http://images.google.com.br/imgres?imgurl=http://upload.wikimedia.org/wikipedia/commons/d/d0/Arco1.png&imgrefurl=http://pt.wikibooks.org/wiki/Matem%25C3%25A1tica_Elementar:_Trigonometria/Arcos_e_%25C3%25A2ngulos&h=194&w=220&sz=12&hl=pt-BR&start=18&sig2=fDPaFgmKyHVMYl9BWwFNLQ&tbnid=aslwKWSNhrr51M:&tbnh=94&tbnw=107&ei=Ku4pSPzxK5eIhQK2yJCaBw&prev=/images%3Fq%3Darcos%2Bc%25C3%25B4ngruos%26gbv%3D2%26hl%3Dpt-BR%26sa%3DG
Esses foram alguns dos exemplos que estudamos fora outras coisas importantes, eu considero que todos aprenderam menos as pessoas que não quiseram mesmo.
Aulas de Matemática
Redução ao 1º quadrante da1ªvolta positiva
*se o arco é do 2º quadrante, o cosseno é negativo e o seno é positivo;
*se o arco é do 3º quadrante, o cosseno é negativo e o seno é negativo;
*se o arco é do 4º quadrante, o cosseno é positivo e o seno é negativo.
Fenômenos Periódicos
Como exemplo podemos usar os movimentos das marés,da radiação eletromagnética, da luz solar e dos pêndulos, todos esses são exemplos de periódicos.
As funções trigonométricas, mais especificamente as senóides são ótimas para descrever esses fenômenos, uma vez que estas são funções periódicas. A forma mais básica de associar as senoides com um movimento periódico é pensar em um ponto que percorre toda a circunferência trigonométrica.Como exemplo pratico, podemos usar a construção de um gráfico (senoide) com tempo e tamanho da sombra solar e horário.
A idéia de seno, cosseno e tangente na circunferência trigonométrica
*O eixo (x)é abscissa cosseno, (y)ordenada seno
aulas diferentes
a professora sara está nos ensinando para nós alunos
contas super criativa.
com as aulas de matematicas eu pude aprender que
o comprimento e medida de arco=a medida de arco é a medida do ângulo central que o subtende,independentimente do raio de circuferencia que contem o arco.
usam-se geralmente unidades como o grau e o radiano para medir o arco
karen caroline 2º B
Por que a circunferencia trigonométrica tem raio 1?
Tal explicação deve ser complementada com a observação de que tomar r=1 corresponde a escolher o (comprimento do) raio como unidade de medida. Como todas as linhas trigonométricas são quocientes entre duas medidas, o valor de cada uma delas se mantém inalterado quando elas passam de uma unidade para outra. Por isso não faz mal convencionar r=1.
No fundo, oque ocorre é que na geometria euclidiana, embora haja uma unidade natural para medir angulo (o radiano) não há uma unidade de comprimento que possa ser escolhida de modo canônico, isto é, independentemente das escolhas arbitrárias. Isso contrasta com a Geometria Hiperbólica (de Lobatchevski e Bolyai), na qual existe uma medida natural para os comprimentos , e portanto para areas e volumes.
trigonometria
Aplicações de trigonometria em nossa vida
Campos que fazem uso da trigonometria ou funções trigonométricas incluem astronomia (especialmente para localização de posições aparentes de objetos celestes, em qual a trigonometria esférica é essencial) e portanto navegação (nos oceanos, em aviões, e no espaço), teoria musical, acústica, óptica, análise de mercado, eletrônica, teoria da probabilidade, estatística, biologia, equipamentos médicos (por exemplo, Tomografia Computadorizada e Ultrassom), farmácia, química, teoria dos números (e portanto criptologia), sismologia, meteorologia, oceanografia, muitas das ciências físicas, solos (inspeção e geodesia), arquitetura, fonética, economia, engenharia, gráficos computadorizados, cartografia, cristalografia e desenvolvimento de jogo.
Uma das aplicações trigonométricas mais conhecidas é a que envolve a área de arquitetura, nas construções de casas,reformas destas,construções de prédios,etc.
Se eu quiser saber a altura de um prédio ou de minha casa, por exemplo, teria que calcular a altura por meio da trigonometria do triângulo retângulo. Se eu fosse uyma engenheira e quisesse saber a largura de um rio para construir uma ponte,meu trabalho seria mais fácil se eu usase os recursos trigonométicos.Se eu fose cartógrafa,demoraria anos para desenhar um mapa sem a ajuda da trigonometria. São posdíveis calcular distância,comprimento,largura,etc,de diversas coisas por meio da trigonometria:a largura de um rio,o compimento de uma rampa,etc.
Podemos utilizar a trigonometria em nossa vida em diversas ocasiões.Ex: Para calcularmos a altura de um muro,para construírmos um rampa em nosas casas,etc.
Se trabalharmos em campos que exigam o uso da trigonometria a utilizaremos com muita freqüência em noso dia-a-dia.
O uso da trigonometria permite que possamos calcular altura, etc,de diversos prédios,casas,etc,com muita mais precisão e facidade. Sem a trigonometria os astrônomos não saberiam a distâncias entre os planetas, um cartógrafo demoraria anos para desenhar um mapa,pontes seriam construídas demoradamente... Enfim, tudo seria bem mais complicado! POR ISSO AS FUNÇÕES TRIGONOMÉTRICAS SÃO TÃO IMPORTANTES EM NOSSA VIDA.
trigonometria no dia-a-dia
conclusão se voçe tivesse noção de trigonometria poderia melhorar as condições de alguem que esta trabalhando paraa voçe como um pedreiro
Aulas diferentes
*Conceitos Trigonométricos. Que explica que um arco simples, faz com que sua circunferência se encontre formando então um arco nulo ou então um arco com uma volta.
*Graus.
Quando dividimos uma circunferência em 360°
Aprendemos diversas outras coisas muito interessantes e que com explicação da professora e também nossas ficou muito mais claro pra o nosso aprendizado.
domingo, 11 de maio de 2008
GERAIS
Contem com suas palavras os assuntos abordados nas aulas.
Podem postar os gráficos feitos nas aulas de informática.
Esse post ainda é válido para o primeiro bimestre, se você não deu sua opinião ou colaboração no primeiro assunto, não perca a chance ( poucos dias)
sábado, 10 de maio de 2008
A trigonometria possui uma infinidade de aplicações práticas. Os antigos já usavam a trigonometria para obter distâncias impossíveis de serem calculadas por métodos comuns.
Algumas aplicações da trigonometria são:
Determinação da altura de um certo prédio.

Seria impossível se medir a distância da Terra à Lua, porém com a trigonometria se torna simples.
Um engenheiro precisa saber a largura de um rio para construir uma ponte, o trabalho dele é mais fácil quando ele usa dos recursos trigonométricos.
Um cartógrafo (desenhista de mapas) precisa saber a altura de uma montanha, o comprimento de um rio, etc. Sem a trigonometria ele demoraria anos para desenhar um mapa.

 Determinação da altura h de uma montanha usando duas sombras de uma vareta de comprimento v.
Determinação da altura h de uma montanha usando duas sombras de uma vareta de comprimento v.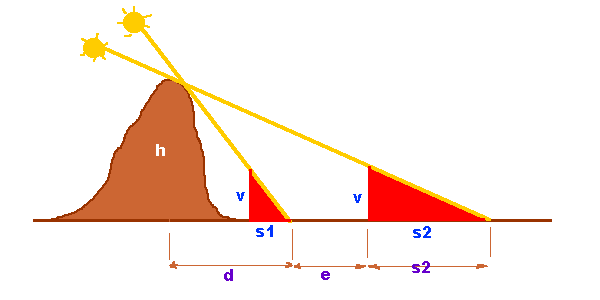

Vejamos mais alguns exemplos a onde a trigonometria está visivelmente presente:
Cálculo da profundidade p de um buraco ( poço, ravina, etc ) usando uma vareta de comprimento v.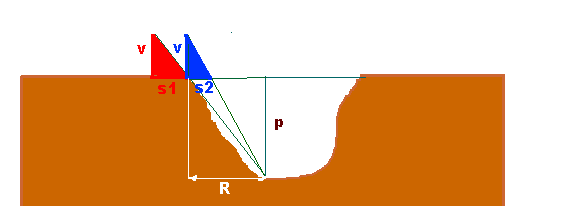
da primeira posição da vareta obtemos: p : R = v : s1
e da segunda posição ( beirada do buraco ) : p : ( R - s2 ) = v : s2, de modo que, após eliminar o R, conseguimos: p = v s2 / ( s2 - s1 )

A trigonometria também é usada para calcular distâncias entre estrelas e planetas.
domingo, 4 de maio de 2008
TIRGONOMETRIA E GEOMETRIA
Em nosso dia-a-dia podemos perceber o uso que obtemos da Matemática, muitas vezes fazemos inconscientemente. Mas dentro deste ramo iremos destacar apenas dois: a TRIGONOMETRIA e a GEOMETRIA.
Para entendemos melhor nosso assunto aqui está o significado de cada uma.
TRIGONOMETRIA: É o ramo da Matemática que trata das relações entre os lados e ângulos de triângulos (polígonos com três lados). A trigonometria plana lida com figuras geométricas pertencentes a um único plano, e a trigonometria esférica trata dos triângulos que são uma seção da superfície de uma esfera. A trigonometria começou como uma Matemática eminentemente prática, para determinar distâncias que não podiam ser medidas diretamente. Serviu à navegação, à agrimensura e à astronomia. Ao lidar com a determinação de pontos e distâncias em três dimensões, a trigonometria esférica ampliou sua aplicação à Física, à Química e a quase todos os ramos da Engenharia, em especial no estudo de fenômenos periódicos como a vibração do som e o fluxo de corrente alternada. A trigonometria começou com as civilizações babilônica e egípcia e desenvolveu-se na Antiguidade graças aos gregos e indianos. A partir do século VIII d.C. astrônomos islâmicos aperfeiçoaram as descobertas gregas e indianas, notadamente em relação às funções trigonométricas. A trigonometria moderna começou com o trabalho de matemáticos no Ocidente a partir do século XV.
GEOMETRIA: Suas origens (do grego medir a terra) parecem coincidir com as necessidades do dia-a-dia. Partilhar terras férteis às margens dos rios, construir casas, observar e prever os movimentos dos astros, são algumas das muitas atividades humanas que sempre dependeram de operações geométricas. Documentos sobre as antigas civilizações egípcia e babilônica comprovam bons conhecimentos do assunto, geralmente ligados à astrologia.
Dentro destes dois ramos da Matemática existem diversas áreas, mas falaremos sobre: seno, cosseno, e tangente dentro da trigonometria, e na geometria falaremos de ângulos.
Minha casa é um sobrado e se encontra em construção, por este motivo resolvi pegar o exemplo do pedreiro para mostrar como eu aprendi seno, cosseno e tangente. Aproveito também e comprovo ao contrário, para aqueles que um pedreiro é ignoran
 te e sem estudos... Sim eles podem não terem estudos, mas são muito inteligentes, pois de uma planta arquitetônica ele é quem faz os cálculos exatos para fazer a obra.
te e sem estudos... Sim eles podem não terem estudos, mas são muito inteligentes, pois de uma planta arquitetônica ele é quem faz os cálculos exatos para fazer a obra.Curiosa perguntei ao pedreiro como ele fez a escada de casa sendo o degrau proporcional ao a ela. Ele disse : " Simples usei trigonometria veja. Primeiro medi a altura ,depois medi a hipotenusa (onde será os degruas), medi da base da hipotenusa até a base da altura (o chão, que é a distância do começo da escada até a coluna) .Todos os degraus tem um tamanho padrão de 20cm, assim é proporcional a escada e não fica cansativo subir ou ceder as escadas. "
Outro caso tamb
 ém é o da parede. Para o pedreiro saber se a parede está nivela ou não ele usa Pitágoras. Primeiro ele mede um lado da parede até 80cm e o outro lado até 60cm, depois ele une com a fita métrica formando um triangulo de 1 metro. Dessa forma a parede está nivelada. Se o resultado da hipotenusa não for 1 metro, a parede não estará nivelada. Veja a imagem ao lado.
ém é o da parede. Para o pedreiro saber se a parede está nivela ou não ele usa Pitágoras. Primeiro ele mede um lado da parede até 80cm e o outro lado até 60cm, depois ele une com a fita métrica formando um triangulo de 1 metro. Dessa forma a parede está nivelada. Se o resultado da hipotenusa não for 1 metro, a parede não estará nivelada. Veja a imagem ao lado.Por acaso alguém se lembra do 3, 4 e 5? Há alguma semelhança?
Para descobrir o lado de um polígono de três lados, mas sabendo que um ângulo é 60º e um lado é tantos metros terei que usar o seno, ou o cosseno, ou a tangente. A famosa tabela que devemos saber décor. Aqui vai um vídeo mostrando como eu decorei esta tabela trigonométrica , dos ângulos 30, 45 e 60 graus.
Aplicação da trigonometria no nosso dia-a-dia
Também usa-se na construção de pontes e prédios.
Algumas aplicações da trigonometria são:
Determinação da altura de um certo prédio.
Os gregos determinaram a medida do raio de terra, por um processo muito simples.
Seria impossível se medir a distância da Terra à Lua, porém com a trigonometria se torna simples.
Um engenheiro precisa saber a largura de um rio para construir uma ponte, o trabalho dele é mais fácil quando ele usa dos recursos trigonométricos.
Um cartógrafo (desenhista de mapas) precisa saber a altura de uma montanha, o comprimento de um rio, etc. Sem a trigonometria ele demoraria anos para desenhar um mapa.
de janelas, etc...
Aplicação da Trigonometria no nosso dia-a-dia
A Trigonometria é um instrumento potente de cálculo, que além de seu uso na Matemática, também é usado no estudo de fenômenos físicos, Eletricidade, Mecânica, Música, Topografia, Engenharia entre outros.
Um pouco da História da Trigonometria:
Trigonometria nasceu c. 300 AC entre os gregos, para resolver problemas de Astronomia Pura . Suas primeiras aplicações práticas ocorrem só com Ptolemaios 150 dC o qual, além de continuar aplicando-a nos estudos astronômicos, a usou para determinar a latitude e longitude de cidades e de outros pontos geográficos em seus mapas.
Do mundo grego, a Trigonometria passou, c. 400 dC, para a India onde era usada nos cálculos astrológicos ( ainda eram problemas de Astronomia ). Por cerca de 800 dC ela chega ao mundo islâmico, onde foi muito desenvolvida e aplicada na Astronomia e Cartografia. Por cerca de 1 100 dC a Trigonometria chegou, junto com os livros de Ptolemaios, na Europa Cristâ. Aí, inicialmente estudada tão somente por suas aplicações na Astronomia, com os portugueses da Escola de Sagres encontra uma aplicação de enorme valor econômico na navegação oceânica.
As aplicações da Trigonometria até c. 1 600 dC :
- Astronomia
- Cartografia
- Navegação Oceânica
A trigonometria é muito utilizada para fazer medições de astros, distâncias, etc. Observando o tamanho angular que observamos os astros da Terra.
Alguns exemplos básicos de aplicações práticas da trigonometria na astronomia:
1º) Eclipses: no cálculo do tamanho da sombra e no cálculo do raio da sombra.
2º) Distâncias dentro do Sistema Solar: calcular distância de planetas inferiores e distâncias de planetas superiores.
3º) Determinação do raio lunar: Um observador com ajuda de aparelhos especiais que lhe forneçam o ângulo em que ele vê a lua e a distância em que a lua se encontra da Terra, pode descobrir o raio da lua, apenas utilizando a lei do seno.
4º) Determinação da distância Terra-Sol: Para calcularmos a distância da Terra ao Sol, devemos, durante o período da fase quarto-crescente da lua, quando o ângulo formado pela Terra, a Lua e o Sol for de 90º, afixar três varetas no chão. Com um transferidor medir o ângulo (abc), calcular os lados do triângulo menor, e depois aplicar regra da semelhança entre triângulos.
Os gregos determinaram a medida do raio de terra, por um processo muito simples.
Seria impossível se medir a distância da Terra à Lua, porém com a trigonometria se torna simples.
Um engenheiro precisa saber a largura de um rio para construir uma ponte, o trabalho dele é mais fácil quando ele usa dos recursos trigonométricos.
Um cartógrafo (desenhista de mapas) precisa saber a altura de uma montanha, o comprimento de um rio, etc. Sem a trigonometria ele demoraria anos para desenhar um mapa.
De acordo com essa pesquisa cheguei a conclusão de que se não for seguir nenhuma dessas profissões a Trigonometria não me sera muito util.
Pesquisei bastanti e realmenti não encontrei se alguém achou por favor me avise pois gostaria de saber como as funções de seno,cosseno e tangente podem ser aplicadas em meu cotidiano.
sábado, 3 de maio de 2008

Existem dois tipos de trigonometria, a Plana e a Esférica, que abordam a resolução de triângulos no plano e na esfera, respectivamente. A trigonometria plana lida com figuras geométricas pertencentes a um único plano, enquanto a trigonometria esférica trata dos triângulos que são uma seção da superficie de uma esfera.

A trigonometria (do grego trigōnon "triângulo" + metron "medida") é um ramo da matematica que estuda os triângulos, particularmente triângulos em um plano onde um dos ângulos do triângulo mede 90 graus (triângulo retangulo). Também estuda especificamente as relações entre os lados e os ângulos dos triângulos; as funções trigonométricas, e os cálculos baseados nelas. A abordagem da trigonometria penetra outros campos da geometria, como o estudo de esferas usando a trigonometra esférica.
A trigonometria possui uma infinidade de aplicações práticas. Desde a antiguidade já se usava da trigonometria para obter distâncias impossíveis de serem calculadas por métodos comuns. Algumas aplicações da trigonometria são:
Determinação da altura de um certo prédio.
Os gregos determinaram a medida do raio de terra, por um processo muito simples.
Seria impossível se medir a distância da Terra à Lua, porém com a trigonometria se torna simples.
Um engenheiro precisa saber a largura de um rio para construir uma ponte, o trabalho dele é mais fácil quando ele usa dos recursos trigonométricos.
Um cartógrafo (desenhador de mapas) precisa saber a altura de uma montanha, o comprimento de um rio, etc. Sem a trigonometria ele demoraria anos para desenhar um mapa.
Na escola mesmo usamos muito a trigonometria (contra nossa vontade), mas isso vai nos ajudar muito pois em vestibulinhos, vestibulares caem muitas pegadinhas nas quais da pra serem resolvidas através da trigonometria.
Na verdade tudo o que aprendemos vai ser util no nosso dia-a-dia as vezes sem percebemos.
Trigonometria
- A Trigonometria é muito importante em nossa vida, é apartir dela que conseguimos novos conhecimentos em muitas áreas, ela poderá ajudar muito em uma carreira profissional no futuro. Tem pessoas que não gostam nem ao menos de escutar falar sobre essa matéria, mais quando for trabalhar em um campo profissional, perceberá o quanto ela será útil. Em nosso dia-a-dia sem percebermos muitas vezes usamos ela, e temos que procurar cada vez mais entendê-la melhor.
sexta-feira, 2 de maio de 2008
Muitas vezes nem notamos, mas a trigonometria é usada no nosso dia-a-dia também.
A trigonometria baseia-se em certas razões, chamadas funções trigonométricas. As aplicações mais antigas das funções trigonométricas eram feitas nas áreas de levantamento topográfico, navegação e engenharia. Estas funções também têm um papel importante no estudo de qualquer fenômeno vibratório - som, luz, electricidade, etc.

A trigonometria, que relaciona as medidas dos lados de um triângulo com as medidas de seus ângulos, é de grande utilidade na medição de distâncias inacessíveis ao ser humano, como a altura de montanhas, torres e árvores, ou a largura de rios e lagos. Encontramos aplicações da Trigonometria na Engenharia, na Mecânica, na Eletricidade, na Acústica, na Medicina, na Astronomia e até na Música.
quinta-feira, 1 de maio de 2008
Entao ÂNGULO RETO É DE 90°
ÂNGULO OBITUSO É AQUELES MAIORES DE 90° E VAI ATE180°
ÂNGULO AGUDO É MENOR DE 90°.
Para os gregos é a quebra de uma reta.
Para os Euclides: "Um ângulo plano é a inclinação recíproca de duas retas que num plano têm um extremo comum e não estão em prolongamento".
*um exemplo de angulo presente em nosso dia a dia é os ponteiros do relogio .
TEOREMA DE TALES
O Teorema de Tales foi proposto pelo filósofo grego Tales de Mileto, e afirma que: quando duas retas transversais cortam um feixe de retas paralelas, as medidas dos segmentos correspondentes determinados nas transversais são proporcionais. Para entender melhor o Teorema de Tales, é preciso saber um pouco sobre razão e proporção. Para a resolução de um problema envolvendo o Teorema de Tales, utiliza-se a propriedade fundamental da proporção, multiplicando-se os meios pelos extremos.
*O Teorema de tales, pode ser aplicado em triângulos que possuem uma reta paralela à um dos lados.
Aulas de Matemática
A aplicação da trigonometria, baseado no triângulo retângulo, se dá na vida prática de várias maneiras. exemplos quando queremos saber a distancia de certa coisas como um prédio casa de uma pessoa enfim em muitas coisas podemos usar a trigonometria.
Tenha um otimo feriado e um bom final de semana Bjoss Jéssica Campos.
ÂNGULOS
Chama-se ângulo, a figura plana limitada por duas semi-retas de mesma origem. Na figura abaixo, podemos observar que as semi-retas OA e OB determinam dois ângulos: um de abertura a (ângulo convexo) e outro de abertura b (ângulo côncavo). O ângulo convexo é indicado por BÔA e a é a medida deste ângulo.
Temos: OA e OB = lados do ângulo e O = vértice do ângulo BÔA.
Medidas de ângulos A principal unidade de medida de ângulos é o grau (símbolo º). Um ângulo raso (aquele formado por duas semiretas opostas, como o mostrado na figura abaixo), mede 180º .
A metade de um ângulo raso, é denominado ângulo reto , e sua medida é 90° .
Concluimos que o ângulo de uma volta completa, corresponde a dois ângulos rasos ou a quatro ângulos retos e portanto sua medida é 360° .
Dividindo-se um ângulo reto em 90 partes iguais, obteremos 90 ângulos de medida 1º cada, sendo portanto 1º a unidade fundamental da medida de ângulos. Esta unidade pode também ser subdividida em unidades menores - o minuto (') e o segundo (") - de forma que:1 grau = 60 minutos e 1 minuto = 60 segundosSimbolicamente: 1º = 60' e 1'= 60"
O uso destas subdivisões do grau, justificam-se nas medidas de ângulos nas quais se requer alto grau de precisão.
Valem ainda, as seguintes definições:
· Ângulo agudo - é aquele cuja medida situa-se entre 0° e 90° .
· Ângulo obtuso - é aquele cuja medida situa-se entre 90° e 180° .
· Ângulos complementares - são aqueles cujas medidas somam 90° . Dizemos que cada um deles é o complemento do outro. Exemplo: 34° é o complemento de 56° e vice-versa , pois 34° + 56° = 90° .
· Ângulos suplementares - são aqueles cujas medidas somam 180° . Dizemos que cada um deles é o suplemento do outro.Exemplo: 48° é o suplemento de 132° e vice-versa, pois 48° + 132° = 180° .
· Ângulos congruentes - são aqueles que possuem medidas iguais. Assim, por exemplo todos os ângulos retos são congruentes, todos os ângulos de medida 60° são congruentes, etc.
· Ângulos opostos pelo vértice - como o próprio nome indica, são aqueles cujos lados de um são os prolongamentos dos lados do outro. Vale aqui, a seguinte proposição, facilmente demonstrável:"Dois ângulos opostos pelo vértice são congruentes, ou seja, possuem a mesma medida".Veja que os ângulos de medidas a e b são congruentes, e, também os ângulos de medidas c e d são também congruentes, ou seja, possuem a mesma medida.
· Retas perpendiculares - são aquelas retas concorrentes (isto é, aquelas que possuem um único ponto em comum) que formam entre si quatro ângulos retos.
Se duas retas r e s são perpendiculares, indicamos isso através do símbolo: r^ s.
· Bissectriz de um ângulo - é a semi-reta que partindo do vértice, determina dois ângulos congruentes ( ou seja, de mesma medida).
Axioma: Todo ângulo, possui uma única bissectriz.
RETAS PARALELAS
Duas retas distintas r e s são paralelas, e indica-se r//s , quando estando contidas num mesmo plano (coplanares) , e não possuem ponto em comum.
Dadas duas retas paralelas, chama-se reta transversal qualquer reta que intercepte ambas as retas. Observamos na figura, que ficam determinados oito ângulos de medidas a, b, c, d, e, f, g e h que recebem denominações especiais a saber:
ângulos correspondentes: b e f, a e e, d e h, e c e g.ângulos alternos internos: d e f, e c e e.ângulos alternos externos: b e h, e a e g.ângulos colaterais internos: d e e, e c e f.ângulos colaterais externos: b e g, e a e h.
Observa-se que:• os ângulos correspondentes são congruentes (medidas iguais)• os ângulos alternos são congruentes (medidas iguais).• os ângulos colaterais são suplementares, isto é, somam 180° .
TRIÂNGULOS
Dados 3 pontos A , B e C , não colineares, isto é , não alinhados , chama-se Triângulo à região do plano limitada pelos segmentos AB , AC e BC , denominados lados , sendo A , B e C os seus vértices. Os ângulos internos são representados por Ð A , Ð B e Ð C , ou simplesmente A , B e C.
Na figura acima, teremos então:
· Soma dos ângulos internos: x + y + z = 180º
· Soma do ângulos externos: E1 + E2 + E3 = 360º
· Em todo triângulo, um ângulo externo é igual à soma dos ângulos internos não adjacentes, ou seja:E1 = y + zE2 = x + yE3 = x + z
Vamos provar as três propriedades acima:
A primeira é imediata, a partir da observação atenta da figura abaixo, se lembrarmos que os ângulos alternos internos possuem a mesma medida. Assim, x = m e y = n. E como sabemos que z + m + n = 180º, vem finalmente: x + y + z = 180º.
Para provar a segunda, basta observar que x + E1 = z + E2 = y + E3 = 180º.Logo, podemos escrever: (x + E1 ) + ( z + E2 ) + ( y + E3 ) = 180º + 180º + 180ºArrumando convenientemente, vem:x + y + z + E1 + E2 + E3 = 540ºE como x + y + z = 180º , substituindo, vem:180º + E1 + E2 + E3 = 540ºDe onde finalmente tiramos: E1 + E2 + E3 = 360º Para provar a terceira, observe que podemos escrever:x + y + z = 180º = x + E1, de onde tiramos: E1 = y + z. Os outros casos, são análogos.
Outra propriedade importante dos triângulos é que a medida de qualquer lado é menor que a soma das medidas dos outros dois.Sendo a , b e c as medidas dos lados de um triângulo qualquer, teremos sempre:a < b + cb < a + cc < a + bconhecidas como Desigualdades Triangulares.
DICA: se um triângulo possui dois lados medindo a e b, o terceiro lado estará compreendido entrea - b e (a + b).Assim, por exemplo, se um triângulo possui dois lados de medidas 10 e 30, o terceiro lado estará compreendido entre 30-10 e 30+10, ou seja, entre 20 e 40.
Os triângulos podem ser classificados quanto à medida dos lados em:
EQUILÁTEROS: medidas dos lados iguais; como consequencia disto , os 3 ângulos internos de um triângulo equilátero são congruentes, isto é , possuem a mesma medida e, portanto cada ângulo mede 60° .
ISÓSCELES: possuem dois lados com medidas iguais. O terceiro lado chama-se base.Verifica-se facilmente, que os ângulos da base de um triângulo isósceles possuem medidas iguais, ou seja, são congruentes.
ESCALENO: possui os tres lados desiguais.
Infere-se , portanto, que todo triângulo equilátero é isósceles, o que significa que o conjunto de todos os triângulos equiláteros é um subconjunto do conjunto de todos os triângulos isósceles.
Os triângulos podem ser classificados quanto às medidas dos ângulos internos , em:
RETÂNGULO: possuem um ângulo reto ( 90° ). O lado oposto ao ângulo reto é chamado hipotenusa e os outros 2 lados, são chamados catetos.
ACUTÂNGULO: todos os ângulos são agudos.
OBTUSÂNGULO: possui um ângulo obtuso.
Elementos lineares de um triângulo.
Mediana - é o segmento que une um vértice ao ponto médio do lado oposto. Conclui-se que todo triângulo possui 3 medianas; o ponto de interseção das 3 medianas de um triângulo, encontram-se em um ponto denominado BARICENTRO ou CENTRO DE GRAVIDADE do triângulo.
Altura - é o segmento que une um vértice ao lado oposto (ou ao prolongamento deste), sendo perpendicular a esse lado. As 3 alturas de um triângulo passam por um mesmo ponto, chamado ORTOCENTRO do triângulo.
Bissectriz interna - é o segmento que divide cada ângulo interno do triângulo, em 2 ângulos iguais. As 3 bissectrizes internas de um triângulo passam por um ponto chamado INCENTRO do triângulo. O incentro é o centro da circunferência inscrita no triângulo, isto é , da circunferência que tangencia os 3 lados do triângulo.
Mediatriz - é a reta perpendicular ao lado, passando pelo ponto médio do mesmo. As 3 mediatrizes de qualquer triângulo passam por um mesmo ponto, chamado CIRCUNCENTRO, que é o centro da circunferência circunscrita ao triângulo, isto é , da circunferência que passa pelos 3 vértices do triângulo.
TEOREMA DE TALES
Um feixe de paralelas determina sobre duas retas transversais quaisquer, segmentos proporcionais. Assim, na figura abaixo, o teorema de Tales nos permite escrever:
O teorema de Tales ( matemático grego, do século VI a.C.) é um dos mais importantes da Geometria, pois, dele, se deduzem como consequências, outros teoremas importantes, como os casos de semelhança de triângulos, o teorema de Pitágoras, etc, temas que serão abordados em breve.
Para encerrar por hoje, vamos resolver a questão a seguir:Na figura abaixo, temos BG//CF//DE. Pede-se calcular o valor de a, b e c, sabendo-se que a soma a + b + c = 45.
Pelo Teorema de Tales, podemos escrever:
Usando uma propriedade das proporções, podemos escrever também:
Portanto, a = 21, b = 9 e c = 15.
Paulo Marques, 31/10/1999 - Feira de Santana - BA.
VOLTAR
Geometria III - Ângulos e Triângulos
ÂNGULOS
Chama-se ângulo, a figura plana limitada por duas semi-retas de mesma origem. Na figura abaixo, podemos observar que as semi-retas OA e OB determinam dois ângulos: um de abertura a (ângulo convexo) e outro de abertura b (ângulo côncavo). O ângulo convexo é indicado por BÔA e a é a medida deste ângulo.
Temos: OA e OB = lados do ângulo e O = vértice do ângulo BÔA.
Medidas de ângulos A principal unidade de medida de ângulos é o grau (símbolo º). Um ângulo raso (aquele formado por duas semiretas opostas, como o mostrado na figura abaixo), mede 180º .
A metade de um ângulo raso, é denominado ângulo reto , e sua medida é 90° .
Concluimos que o ângulo de uma volta completa, corresponde a dois ângulos rasos ou a quatro ângulos retos e portanto sua medida é 360° .
Dividindo-se um ângulo reto em 90 partes iguais, obteremos 90 ângulos de medida 1º cada, sendo portanto 1º a unidade fundamental da medida de ângulos. Esta unidade pode também ser subdividida em unidades menores - o minuto (') e o segundo (") - de forma que:1 grau = 60 minutos e 1 minuto = 60 segundosSimbolicamente: 1º = 60' e 1'= 60"
O uso destas subdivisões do grau, justificam-se nas medidas de ângulos nas quais se requer alto grau de precisão.
Valem ainda, as seguintes definições:
· Ângulo agudo - é aquele cuja medida situa-se entre 0° e 90° .
· Ângulo obtuso - é aquele cuja medida situa-se entre 90° e 180° .
· Ângulos complementares - são aqueles cujas medidas somam 90° . Dizemos que cada um deles é o complemento do outro. Exemplo: 34° é o complemento de 56° e vice-versa , pois 34° + 56° = 90° .
· Ângulos suplementares - são aqueles cujas medidas somam 180° . Dizemos que cada um deles é o suplemento do outro.Exemplo: 48° é o suplemento de 132° e vice-versa, pois 48° + 132° = 180° .
· Ângulos congruentes - são aqueles que possuem medidas iguais. Assim, por exemplo todos os ângulos retos são congruentes, todos os ângulos de medida 60° são congruentes, etc.
· Ângulos opostos pelo vértice - como o próprio nome indica, são aqueles cujos lados de um são os prolongamentos dos lados do outro. Vale aqui, a seguinte proposição, facilmente demonstrável:"Dois ângulos opostos pelo vértice são congruentes, ou seja, possuem a mesma medida".Veja que os ângulos de medidas a e b são congruentes, e, também os ângulos de medidas c e d são também congruentes, ou seja, possuem a mesma medida.
· Retas perpendiculares - são aquelas retas concorrentes (isto é, aquelas que possuem um único ponto em comum) que formam entre si quatro ângulos retos.
Se duas retas r e s são perpendiculares, indicamos isso através do símbolo: r^ s.
· Bissectriz de um ângulo - é a semi-reta que partindo do vértice, determina dois ângulos congruentes ( ou seja, de mesma medida).
Axioma: Todo ângulo, possui uma única bissectriz.
RETAS PARALELAS
Duas retas distintas r e s são paralelas, e indica-se r//s , quando estando contidas num mesmo plano (coplanares) , e não possuem ponto em comum.
Dadas duas retas paralelas, chama-se reta transversal qualquer reta que intercepte ambas as retas. Observamos na figura, que ficam determinados oito ângulos de medidas a, b, c, d, e, f, g e h que recebem denominações especiais a saber:
ângulos correspondentes: b e f, a e e, d e h, e c e g.ângulos alternos internos: d e f, e c e e.ângulos alternos externos: b e h, e a e g.ângulos colaterais internos: d e e, e c e f.ângulos colaterais externos: b e g, e a e h.
Observa-se que:• os ângulos correspondentes são congruentes (medidas iguais)• os ângulos alternos são congruentes (medidas iguais).• os ângulos colaterais são suplementares, isto é, somam 180° .
TRIÂNGULOS
Dados 3 pontos A , B e C , não colineares, isto é , não alinhados , chama-se Triângulo à região do plano limitada pelos segmentos AB , AC e BC , denominados lados , sendo A , B e C os seus vértices. Os ângulos internos são representados por Ð A , Ð B e Ð C , ou simplesmente A , B e C.
Na figura acima, teremos então:
· Soma dos ângulos internos: x + y + z = 180º
· Soma do ângulos externos: E1 + E2 + E3 = 360º
· Em todo triângulo, um ângulo externo é igual à soma dos ângulos internos não adjacentes, ou seja:E1 = y + zE2 = x + yE3 = x + z
Vamos provar as três propriedades acima:
A primeira é imediata, a partir da observação atenta da figura abaixo, se lembrarmos que os ângulos alternos internos possuem a mesma medida. Assim, x = m e y = n. E como sabemos que z + m + n = 180º, vem finalmente: x + y + z = 180º.
Para provar a segunda, basta observar que x + E1 = z + E2 = y + E3 = 180º.Logo, podemos escrever: (x + E1 ) + ( z + E2 ) + ( y + E3 ) = 180º + 180º + 180ºArrumando convenientemente, vem:x + y + z + E1 + E2 + E3 = 540ºE como x + y + z = 180º , substituindo, vem:180º + E1 + E2 + E3 = 540ºDe onde finalmente tiramos: E1 + E2 + E3 = 360º Para provar a terceira, observe que podemos escrever:x + y + z = 180º = x + E1, de onde tiramos: E1 = y + z. Os outros casos, são análogos.
Outra propriedade importante dos triângulos é que a medida de qualquer lado é menor que a soma das medidas dos outros dois.Sendo a , b e c as medidas dos lados de um triângulo qualquer, teremos sempre:a < b + cb < a + cc < a + bconhecidas como Desigualdades Triangulares.
DICA: se um triângulo possui dois lados medindo a e b, o terceiro lado estará compreendido entrea - b e (a + b).Assim, por exemplo, se um triângulo possui dois lados de medidas 10 e 30, o terceiro lado estará compreendido entre 30-10 e 30+10, ou seja, entre 20 e 40.
Os triângulos podem ser classificados quanto à medida dos lados em:
EQUILÁTEROS: medidas dos lados iguais; como consequencia disto , os 3 ângulos internos de um triângulo equilátero são congruentes, isto é , possuem a mesma medida e, portanto cada ângulo mede 60° .
ISÓSCELES: possuem dois lados com medidas iguais. O terceiro lado chama-se base.Verifica-se facilmente, que os ângulos da base de um triângulo isósceles possuem medidas iguais, ou seja, são congruentes.
ESCALENO: possui os tres lados desiguais.
Infere-se , portanto, que todo triângulo equilátero é isósceles, o que significa que o conjunto de todos os triângulos equiláteros é um subconjunto do conjunto de todos os triângulos isósceles.
Os triângulos podem ser classificados quanto às medidas dos ângulos internos , em:
RETÂNGULO: possuem um ângulo reto ( 90° ). O lado oposto ao ângulo reto é chamado hipotenusa e os outros 2 lados, são chamados catetos.
ACUTÂNGULO: todos os ângulos são agudos.
OBTUSÂNGULO: possui um ângulo obtuso.
Elementos lineares de um triângulo.
Mediana - é o segmento que une um vértice ao ponto médio do lado oposto. Conclui-se que todo triângulo possui 3 medianas; o ponto de interseção das 3 medianas de um triângulo, encontram-se em um ponto denominado BARICENTRO ou CENTRO DE GRAVIDADE do triângulo.
Altura - é o segmento que une um vértice ao lado oposto (ou ao prolongamento deste), sendo perpendicular a esse lado. As 3 alturas de um triângulo passam por um mesmo ponto, chamado ORTOCENTRO do triângulo.
Bissectriz interna - é o segmento que divide cada ângulo interno do triângulo, em 2 ângulos iguais. As 3 bissectrizes internas de um triângulo passam por um ponto chamado INCENTRO do triângulo. O incentro é o centro da circunferência inscrita no triângulo, isto é , da circunferência que tangencia os 3 lados do triângulo.
Mediatriz - é a reta perpendicular ao lado, passando pelo ponto médio do mesmo. As 3 mediatrizes de qualquer triângulo passam por um mesmo ponto, chamado CIRCUNCENTRO, que é o centro da circunferência circunscrita ao triângulo, isto é , da circunferência que passa pelos 3 vértices do triângulo.
TEOREMA DE TALES
Um feixe de paralelas determina sobre duas retas transversais quaisquer, segmentos proporcionais. Assim, na figura abaixo, o teorema de Tales nos permite escrever:
O teorema de Tales ( matemático grego, do século VI a.C.) é um dos mais importantes da Geometria, pois, dele, se deduzem como consequências, outros teoremas importantes, como os casos de semelhança de triângulos, o teorema de Pitágoras, etc, temas que serão abordados em breve.
Para encerrar por hoje, vamos resolver a questão a seguir:Na figura abaixo, temos BG//CF//DE. Pede-se calcular o valor de a, b e c, sabendo-se que a soma a + b + c = 45.
Pelo Teorema de Tales, podemos escrever:
Usando uma propriedade das proporções, podemos escrever também:
Portanto, a = 21, b = 9 e c = 15.
Paulo Marques, 31/10/1999 - Feira de Santana - BA.
VOLTAR



